¿Por qué la Luna no tiene atmósfera?

¿Por qué la Luna no tiene atmósfera, si se encuentra casi a la misma distancia del Sol que la Tierra? Para responder a esta pregunta, vamos a ver un modelo de física básica que primero nos dará la velocidad a la que hay que lanzar una pelota para que escape de nuestro planeta. Empecemos con la segunda cuestión, en la que aprenderemos de qué depende que algo escape de su planeta o satélite. Para responder a esa pregunta, debemos relacionar la velocidad a la que lo lancemos con la atracción gravitatoria del planeta.

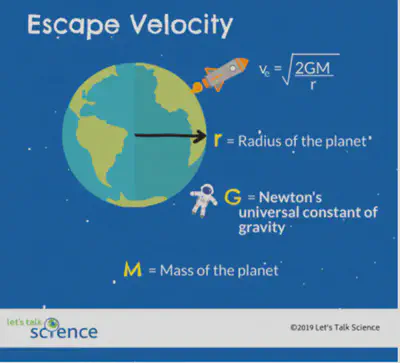
Como en mi entrada del hielo y la rotación de la Tierra, hay que hacer aproximaciones de vaca esférica para simplificar el problema. Asumimos que la Tierra es una esfera homogénea y no tenemos en cuenta el rozamiento del aire ni la rotación del planeta sobre sí mismo. Para obtener la velocidad de escape igualamos la energía cinética de la pelota con su energía gravitatoria¹:

\begin{gather*} \overbrace{E_\mathrm c = \frac{1}{2}mv^2}^{\text{Energía cinética}}; \qquad \overbrace{E_\mathrm p = -\frac{GmM_\mathrm T}{R_\mathrm T}}^{\text{Energía potencial gravitatoria}} \\ E_\mathrm{sist} = 0 \Rightarrow v_\mathrm{escape} = \sqrt{\frac{2GM_\mathrm T}{R_\mathrm T}} \end{gather*}

Un tema relacionado con esto es el rango de velocidades para poner un objeto en órbita en torno a su planeta. En este hilo, Antonio J. Cuesta lo explica de forma intuitiva:

Sigamos con nuestra entrada y analicemos la velocidad de escape de nuestro planeta. Para la Tierra obtenemos una velocidad de escape de 11.2 km/s, 33 veces la velocidad del sonido en el aire. Cualquier objeto lanzado a menor velocidad caerá de nuevo. Como veis, el valor depende de la masa del planeta, M, y de su radio, R: hace falta una mayor velocidad a mayor M y menor R.

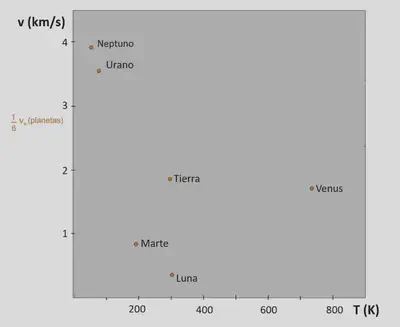
Quizá lo más interesante sea de qué NO depende la velocidad de escape. En este modelo NO depende de la masa del objeto que lanzamos². Por tanto, en la gráfica de debajo, que ampliaremos más adelante, cada planeta (punto naranja) tiene su velocidad de escape (eje y).

Ahora vamos a usar las velocidades de escape que hemos obtenido como límite para que un planeta retenga sus átomos o moléculas de gas. Nos toca preguntarnos ahora a qué velocidad promedio circulan las moléculas de distintos gases para saber si el planeta los podrá retener o no.

Los átomos o moléculas del gas siguen una distribución estadística de velocidades en torno a cierta velocidad de traslación promedio <v>. Aplicando la teoría cinética se llega a la expresión de debajo, donde se deduce que cuanto menor masa tenga la molécula, en promedio más rápido viajará.

$$ \frac{3k_\mathrm B T}{2} = \frac{1}{2}m\langle v\rangle^2 \rightarrow \langle v\rangle = \sqrt{\frac{3k_\mathrm B T}{m}} $$

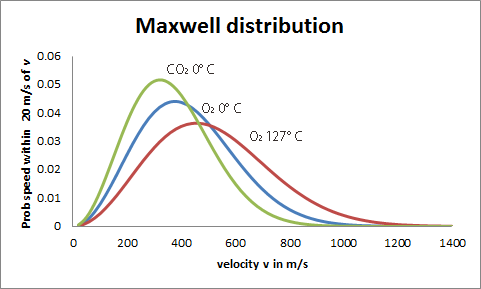
Resumiendo, la velocidad mínima para que una partícula escape del planeta depende de propiedades del planeta, pero no de la masa de la partícula. Por otro lado, cada tipo de molécula de gas viaja en promedio a cierta velocidad dada por su masa y la temperatura a la que esté:

$$ v_\mathrm{escape} = \sqrt{\frac{2GM}{R}}; \qquad \langle v\rangle = \sqrt{\frac{3k_\mathrm B T}{m}} $$

Con eso representamos la figura 1 y comparamos la velocidad promedio de las moléculas con 1/6 de la velocidad de escape: el planeta retendrá aquellas cuya línea quede por debajo de su punto naranja. Esto nos da algunas claves para su composición atmosférica:

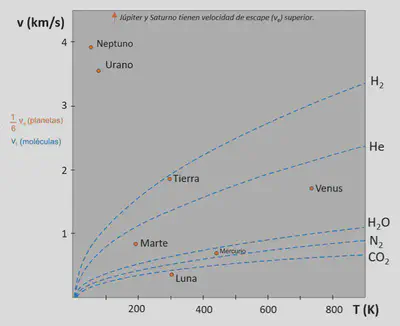
Con este modelo, resumido en la gráfica anterior, es comprensible que las atmósferas de Júpiter o Saturno sean principalmente de H₂ y He (lo más común en el Universo) mientras que, como estos gases escapan fácilmente de Venus o la Tierra, queden atmósferas de gases más pesados.

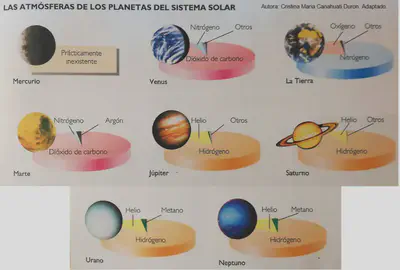
El planeta de nuestro sistema solar con menor velocidad de escape, Mercurio, a efectos prácticos no tiene atmósfera. Marte tiene una atmósfera muy tenue, cuya presión es de unos 600 Pa, menos del 1 % respecto a la de la Tierra (una atmósfera residual, como me apuntó mi amigo el astrofísico Rodrigo González Peinado). Los planetas terrestres tienen una velocidad de escape menor que la de los planetas jovianos, lo que les ha impedido retener grandes cantidades de hidrógeno y helio.

¿Y la Luna? Aunque su temperatura sea similar a la de la Tierra, debido a su menor masa/radio, su velocidad de escape es menor (2.4 km/s vs 11.2 km/s). Las moléculas de los principales gases escapan rápidamente y, por ello, no puede retener una atmósfera con ellas.

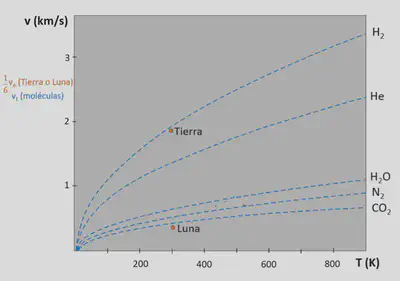
Así terminaría esta entrada sobre la velocidad de escape, donde hemos empezado viendo a qué velocidad hay que lanzar una pelota para que escape de la Tierra para terminar entendiendo por qué la Luna no retiene apenas gases a su alrededor. Un momento…, ¿por qué escribo apenas?

via GIPHY

Porque, aunque a efectos prácticos la Luna no tiene atmósfera por lo visto en esta entrada, si uno mide la composición gaseosa sobre su superficie, encuentra mayormente argón, helio y neón, si bien la presión es un billón (10¹²) de veces menor que en la atmósfera terrestre.

Si bien estos elementos gaseosos no aguantan mucho tiempo en la Luna, se ven reemplazados por nuevos, emitidos por el propio satélite.