El origen del color del oro

¿Alguna vez te has preguntado por qué el oro tiene ese color tan característico en lugar del color plateado de la mayoría de los metales? Hoy vamos a adentrarnos en el mundo de la mecánica cuántica y la relatividad para desentrañar la respuesta.

En un átomo, los electrones se encuentran en niveles energéticos muy bien definidos. Como podéis ver en la imagen, los electrones absorberán o emitirán energía exactamente igual a la diferencia entre niveles. Cuando la emisión de energía cae en el rango visible, vemos un color:

El color del oro no se puede explicar a partir de los niveles electrónicos del átomo de Au aislado, ya que en el oro metálico tenemos muchos de estos átomos fuertemente enlazados entre sí, formando una estructura cristalina cúbica centrada en las caras:

Veamos cómo pasar del átomo al sólido con la molécula de hidrógeno (H₂). Uno primero colocaría dos diagramas energéticos idénticos, uno para cada átomo. Sin embargo, la interacción electrostática entre ellos modifica las energías electrónicas, formando orbitales moleculares:

En la molécula de H₂ los dos electrones ocupan el orbital de menor energía de los dos disponibles, llamado enlazante. Se requiere mucha energía para excitar los electrones al otro orbital. Sin embargo, según juntamos más átomos la diferencia energética se va reduciendo. Por ejemplo, mirad el nivel 3s del sodio. En un átomo está semilleno (1 de 2 electrones), en una molécula de Na₂ ambos están en el orbital enlazante y, cuando tenemos muchos, los orbitales están tan cerca que lo llamamos banda, que en el sodio está semillena de electrones:

Ya no tenemos energías discretas; los electrones con más energía disponen de niveles vacíos donde acceder a muy poca energía de la suya. Haciendo una analogía clásica, es como pasar de tener que saltar un muro a disponer de una rampa. Cuando esto ocurre, tenemos un metal. Resumiendo, en un metal habrá cierta banda de energía semillena de electrones (e^–). El e^– con mayor energía se encuentra (a T = 0 K) en el nivel de Fermi. Los e^– pueden acceder a niveles de E justo encima de donde se encuentran; por eso son buenos conductores de electricidad:

Cuando enviábamos luz a un átomo, éste solo absorbía ciertas energías, dadas por las diferencias entre sus niveles energéticos. Con los metales habituales, la radiación de cualquier energía visible (todos los colores de la luz) es brevemente absorbida, por lo que hemos visto:

Uno pensaría entonces que, si absorben cualquier fotón visible, los metales deberían ser negros. Sin embargo, en estos metales el electrón excitado vuelve a su nivel original casi instantáneamente, emitiendo luz de la misma energía (color) que ha absorbido. Esto hace que los metales sean perfectamente reflectantes, siempre que estén muy pulidos. De hecho, los espejos en nuestras casas muestran nuestra imagen reflejada no por el vidrio sino por la lámina pulida de metal (p. ej. plata) que contienen detrás:

La estructura electrónica que hemos visto explica que la mayoría de los metales no pulidos sean plateados, al reflejar la luz de todos los colores. Sin embargo, el oro sí devuelve cierto color, uno que además nos ha fascinado históricamente. ¿Qué cambia en el oro?

Veamos los espectros de reflectancia de distintos metales. Mientras que la plata y el aluminio son muy reflectantes en todas las energías visibles, el oro solo refleja luz de altas longitudes de onda (por tanto, de bajas energías):

Esta explicación está bien, pero solo te he mostrado una medida experimental que se corresponde con el color del oro; no he entrado en su origen fundamental. ¿Por qué para entender el color de un metal como el oro no nos sirve con usar el diagrama habitual de un metal, una banda de energía semillena de electrones?

Veamos dónde está el oro en la tabla periódica. Como veis, se encuentra en la misma columna que la plata, pero una fila por debajo. Ambos tienen un electrón desapareado en el orbital s más externo, pero el oro tiene muchos más protones (79 frente a 47 de la plata):

Al haber más protones, los electrones en los orbitales se ven más atraídos hacia el núcleo. Por ejemplo, usando el modelo de Bohr se puede calcular que la velocidad de los electrones en la órbita 1s del oro sería más del 50% de la velocidad de la luz:

$$ \frac{Ze^2}{4\pi\epsilon_0 r^2} = m_\mathrm e \frac{v^2}{r} $$

He escrito “sería” porque este modelo parte de la mecánica clásica y, a estas velocidades relativistas (cercanas a la velocidad de la luz), hay que meterse en otro jardín, el de la relatividad especial de Einstein. Solo podemos entender el color del oro a partir de ella. Vamos a ver el concepto clave de relatividad para entender la consecuencia de tener electrones tan veloces. Fijaos cómo la energía cinética que requiere una partícula con masa para viajar a velocidades cercanas a la luz es mayor que la predicha por la mecánica clásica:

Es decir, algunos electrones (–) en el oro, debido al mayor número de protones (+) en su núcleo, viajan a velocidades relativistas, dando lugar no a que sean “más masivos”, como aparece en algunas fuentes, sino a que su energía sea mayor. ¿De qué electrones estamos hablando? De los de la banda 6s semillena, que son los que interactúan con la luz visible y UV. Pero, un momento, en clase me enseñaron que los niveles más externos del oro que dan lugar a esa banda, los 6s, están lejos del núcleo y por tanto no deberían ser muy afectados por esto…

La clave está en que el modelo atómico más cercano a la realidad no es el de Bohr, que aparece en la mayoría de imágenes de Internet, sino el mecánico-cuántico. Ahí, los electrones en orbitales “s” superiores también tienen cierta probabilidad de encontrarse cerca del núcleo:

Así, debido a la alta velocidad de los electrones en la banda 6s del oro, éstos tienen una energía mayor que la predicha por el modelo atómico no relativista. Esto ocurre en muchos otros elementos y materiales, pero el efecto suele ser mínimo y no afecta a su emisión de luz. Este efecto, presente en orbitales “s” y “p”, se denomina contracción relativista, para indicar que es más probable encontrar a esos electrones más cerca del núcleo de lo predicho. Fue desarrollado por uno de los padres del modelo atómico, Arnold Sommerfeld, en 1916:

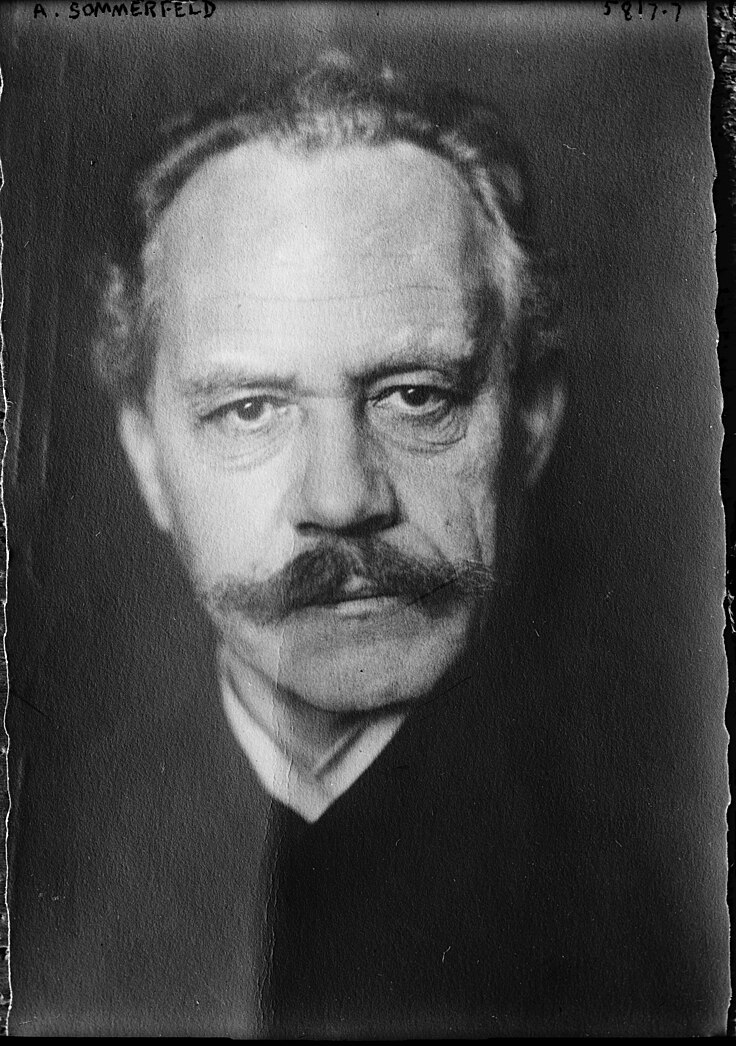
Bien, espero haberos convencido de que los electrones de la banda 6s del oro viajan a velocidades relativistas, desplazando por tanto la banda 6s a mayor energía. Pero, volviendo al diagrama de antes del metal de una banda, seguimos sin poder explicar su emisión de luz…

En realidad, en el oro tenemos dos bandas de energía que participan en el negocio en vez de una, que provienen de orbitales muy cerca energéticamente entre sí; el 5d y el 6s. Ahí sí, lo que hemos visto explica la particularidad del oro; fijaos en el diagrama de sus bandas:

Ese diagrama es como el de la banda semillena de electrones de antes, solo que la banda 5d, que está completamente llena de electrones (por eso está toda coloreada), se encuentra por relatividad suficientemente cerca de la 6s para absorber, p. ej., fotones visibles verdes (2.4 eV). Hemos visto que la alta velocidad explica el aumento de la energía (negativa, pues se trata de una energía de enlace) de los electrones 6s. Este efecto relativista se ha calculado para la molécula de AuH, como veis en la siguiente figura:

Algo análogo ocurre con el oro metálico. Fijaos también en la figura anterior que en los niveles 5d ocurre lo contrario que en el 6s. Esto es una característica general y se debe a que los niveles s relativistas apantallan más a los d, generando el efecto contrario. Bien, comparemos ahora al oro con la plata. Mientras que en el oro hay absorciones de luz por transiciones 5d–6s en el rango visible, la diferencia entre los niveles 5s y 4d de la plata apenas requiere corrección relativista y se mantiene en el ultravioleta, por encima de los 3.1 eV de la luz visible más energética:

Volviendo al espectro de reflectancia, ahora entendemos la caída de reflectancia en el oro a partir del amarillo; la luz verde y azul es suficientemente energética para ser absorbida por electrones de la banda 5d. En la plata, eso empieza a ocurrir en el UV (<350 nm):

Con esto termina la entrada, más densa que lo habitual pero que, a cambio, nos da un ejemplo visual que ayuda a profundizar en conceptos de las dos mayores revoluciones de la física del siglo XX. Si has leído hasta aquí, gracias por tu tiempo y esfuerzo; dale mucha difusión. 😊

via GIPHY

Espero que la entrada os haya mostrado lo bonita y compleja que puede llegar a ser la física del estado sólido para explicar algo tan cercano como el color del oro.