Esto es Física

Índice

1. Lengua española PRESIÓN

El que mucho abarca, poco aprieta.

$$ p = \frac{F}{S}, $$

lo que nos permite explicar el famoso refrán, pues efectivamente a mayor superficie, menor es la presión ejercida.

2. Inglés DISPERSIÓN

En este capítulo se nos presenta la importante diferencia entre la dispersión refractiva, como la que ocurre en un prisma o en las gotas de agua para formar el arcoíris; y la dispersión de Rayleigh, que nos permite explicar por qué vemos el cielo azul.

Aprende más sobre la reflexión y la refracción de la luz con esta excelente simulación:

3. Filosofía HORROR VACUI

Este capítulo explora el concepto del vacío y sus efectos en la ebullición de líquidos, la expansión de gases o la caída de graves¹.

¿Sabes que horror vacui es también el título de un podcast?

El propio Departamento de Física y Química del IES Valle del Saja, junto con algunos/as amigos/as y docentes de Secundaria, tiene un podcast titulado precisamente Horror vacui, mediante el que, de momento, han hecho su particular homenaje a los 50 años del viaje a la Luna.

Disponible en Spotify:

y en Ivoox:

4. Música TIMBRE

Este capítulo detalla la importancia del timbre, esa cualidad del sonido que nos permite distinguir un instrumento musical de otro gracias a su característico espectro (intensidad relativa de sus distintos armónicos).

5. Dibujo ELIPSES

Este capítulo trata sobre las secciones cónicas y, en particular, la elipse y su importancia en Física:

Aprende más sobre gravedad y órbitas, el Sistema Solar o las leyes de Kepler con las siguientes simulaciones de PhET Colorado:

6. Educación Física EQUILIBRIO

Capítulo dedicado al equilibrio y sus tres tipos según su definición basada en la energía potencial: estable, inestable e indiferente ( o neutro):

Aprende más sobre la ley del equilibrio con esta excelente simulación:

7. Latín/griego BRAQUISTÓCRONA

Este capítulo nos presenta el famoso problema de encontrar la curva que minimiza el tiempo de caída de un objeto entre dos puntos no alineados, bajo la única influencia de la gravedad (sin rozamiento). Esta curva recibe el nombre de braquistócrona, que fue uno de los primeros problemas planteados en el cálculo de variaciones, siendo resuelto por Newton en 1697.

El tiempo que se tarda en viajar de un punto $P_1$ a otro $P_2$ viene dado por la integral:

$$ t_{12} = \int_{P_1}^{P_2} \frac{\mathrm d s}{v}, $$

donde $s$ es la longitud del arco y $v$ la velocidad, la cual puede relacionarse con $y$ utilizando la conservación de la energía mecánica (recordemos que solo actúa la gravedad que es una fuerza conservativa):

$$ \frac{1}{2}mv^2 = mgy \Rightarrow v = \sqrt{2gy} $$

Notamos también que:

$$ \mathrm d s = \sqrt{\mathrm d x^2 + \mathrm d y^2} = \sqrt{1+y'^2}\,\mathrm d x, $$

por lo que podemos escribir el tiempo $t_{12}$ como:

$$ t_{12} = \int_{P_1}^{P_2} \sqrt{\frac{1+y'^2}{2gy}}\,\mathrm d x $$

Tras un poco de cálculo basado en la ecuación de Euler-Lagrange², se llega a una solución en términos de ecuaciones paramétricas³:

$$ \begin{aligned} x &= \frac{1}{2}k^2 (\theta-\sin\theta) \\ y &= \frac{1}{2}k^2 (1-\cos\theta) \end{aligned} $$

que resultan ser las ecuaciones de una cicloide ($k$ es una constante positiva).

Puede demostrarse que la curva braquistócrona se trata también de una curva tautócrona o isócrona, lo que significa que el tiempo que tarda el objeto en llegar hasta su punto más bajo es independiente de su punto de partida:

8. Matemáticas TRIGONOMETRÍA

En este capítulo se nos muestra cómo distintos fenómenos cotidianos, como las oscilaciones de un péndulo:

o las vibraciones de una cuerda atada por los dos extremos:

involucran funciones trigonométricas, haciendo hincapié en la función seno.

9. Francés PASCAL

En este cortometraje-documental del propio Departamento de Física y Química del IES Valle del Saja “se somete a diversas revisiones el controvertido experimento conocido como tonel de Pascal”, ideado por el propio Pascal para demostrar de forma definitiva el principio que lleva su nombre:

Además, con esta simulación puedes comprobar cómo la presión que ejerce un fluido depende únicamente de la profundidad a la que nos encontremos, algo que se conoce como la paradoja hidrostática:

10. Tecnología ÓPTICA

Aprende a explicar cómo se forma una imagen mediante una lente convergente/divergente o un espejo utilizando diagramas de rayos, gracias a esta excelente simulación:

11. Orientación MAGNETISMO

Este capítulo nos recuerda la experiencia de Ørsted, que demostró que las corrientes eléctricas crean campos magnéticos:

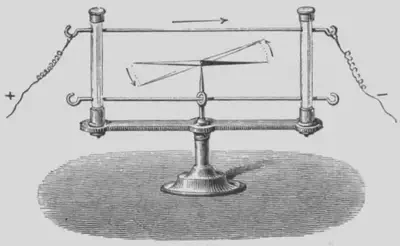
12. Economía ELECTRICIDAD

En este caso se nos presenta la experiencia de Faraday-Henry, que demostró que los campos magnéticos pueden crear corrientes eléctricas:

Puedes aprender más jugando con esta simulación:

Ambas experiencias (Ørsted y Faraday-Henry) pusieron de manifiesto la estrecha relación que existe entre los fenómenos eléctricos y magnéticos, dando origen al electromagnetismo.

13. Geografía CAMBIO CLIMÁTICO

Manuel Alonso Orts escribía recientemente esta magnífica entrada de blog, donde discute los motivos por los que está subiendo el nivel del mar.

14. Física PÉNDULO DE NEWTON

Este capítulo explora el conocido como péndulo o cuna de Newton, dispositivo que demuestra la conservación del momento lineal y la conservación de la energía con esferas oscilantes:

Fue diseñado por el físico francés del siglo XVII Edme Mariotte y, en sus Principia, el propio Isaac Newton menciona los experimentos realizados por el físico francés.

Aprende más sobre colisiones con este excelente laboratorio virtual:

15. Química BUZO DE DESCARTES

Este capítulo nos presenta el conocido como buzo de Descartes, un dispositivo que pone en juego hasta 4 leyes de la Física: el principio de Arquímedes (flotabilidad), el principio de Pascal, la ley de Boyle (gases ideales) y la ley fundamental de la dinámica (segunda ley de Newton).

16. Biología ROBERT HOOKE

Este capítulo trata sobre la figura de Robert Hooke y, en especial, su famosa ley de la elasticidad, que relaciona el alargamiento o elongación, $\Delta l$, que sufre un muelle o resorte bajo la acción de una cierta fuerza $F$:

$$ F = k\cdot \Delta l, $$

donde $k$ es la llamada constante de elasticidad del muelle. Como se puede ver en la figura, el alargamiento sufrido por el muelle es proporcional a la fuerza ejercida sobre él.

Puedes aprender más sobre masas, resortes y la ley de Hooke con las siguientes simulaciones: